Physics 2212, Sim 08: Capacitance and RC Circuits

Eric Murray, Summer 2020

Question these experiments will enable you to answer: Is the capacitance of your simulated capacitor the ratio of the charge on it to the potential across it? What is the time constant of your simulated RC circuit?

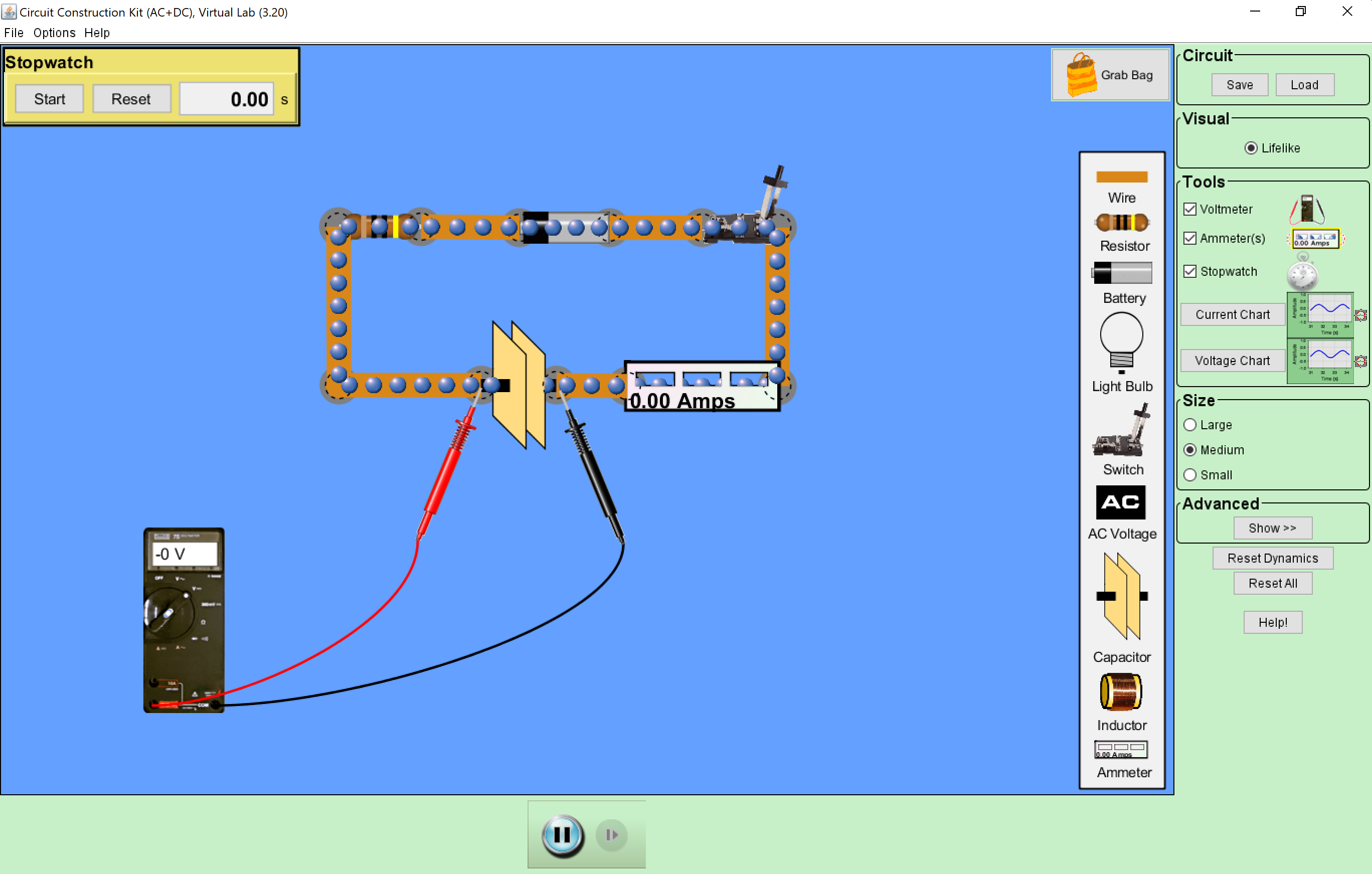
Features: The simulated circuit consists of a battery, switch, capacitor, and ammeter in series. A voltmeter measures the potential across the capacitor. Capacitor charge is calculated by approximating the integral of the current with respect to time. Capacitance is calculated as the slope of a charge vs. potential difference plot.

Next, time constant is investigated. Fitting a linear curve to the appropriate function of current as it depends on time, enables the time constant of the circuit to be calculated.

Preliminaries: Open the Circuit Construction Kit (AC+DC), Virtual Lab with Java, or select Lab in the HTML5 prototype. Build a simulated series RC circuit, including a switch and an ammeter. Use a voltmeter to measure the potential across the capacitor. There are many valid ways to build this circuit, but an example is illustrated (and linked to a larger image). Set the battery emf, capacitance, and resistance to 100 V, 0.2 F, and 100 Ω, respectively. Enable the stopwatch.

Experiment 1: Pause (❘❘) the simulation, start the stopwatch, close the switch. Play (▶) the simulation, then pause it immediately. Record the time, the potential across the capacitor, and the current. Note that the stopwatch keeps simulation time, not real time.

Repeatedly Play and Pause the simulation to record measurements approximately every second for 10 seconds. Then record measurements approximately every two seconds for the next 10 seconds. Finally, record measurements approximately every five seconds for the next 40 seconds.

Calculate theoretical values for the current, capacitor charge, and capacitor potential at time t = 0. Find the charge ΔQ added to the capacitor in each time interval by approximating the current as its constant average value during that time interval. Find the charge on the capacitor at each time. The ratio of this charge to the capacitor potential at that time is the capacitance.

Find the capacitance of your simulated capacitor from these 24 measurements, with its experimental uncertainty.

Experiment 2: Using the data already collected, calculate -ln(I/I₀) for each measurement. As seen in the prelab, this should be a linear function of time. Confirm this with a graph. Use linear regression to determine the slope and its uncertainty. From that slope, calculate the time constant of your circuit.

Summary: Review your worksheet. Think about the goals of these experiments, your results, and expectations from while writing your discussion.