Eric Murray, Fall 2006
Coulomb's Law describes the electrostatic force, F, between point particles carrying charges Q and q and separated by a distance r. Dividing the charge values q yields an expression for the electric field, E, due to the particle with charge Q. In terms of magnitudes
F = kQq / r2 ⇒ F / q = E = kQ / r2
where k is 1/4πε0.
Once an expression for the electric field in known, then an electric potential difference, ΔV between two points can be determined according to
ΔV = -∫E⋅ds
where ds is an element of the path between the points. Alternately, if an expression for V is known, then the electric field can be determined an any point
Es = -∂V / ∂s
The sign of the field simply indicates its direction, which is toward lower potential.
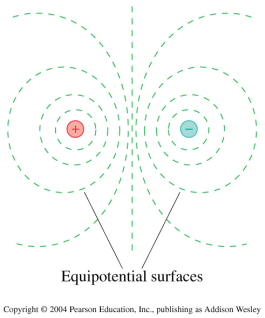
Experimentally, the electric potential at a point (really the electric potential difference between that point and an arbitrary reference point) is relatively easy to determine, by using a voltmeter. A collection of points with the same electric potential constitute an equipotential surface. The electric field must be perpendicular to every equipotential surface, and the field magnitude may be approximated by a difference ratio (rather than a derivative)
Es ≈ ΔV / Δs
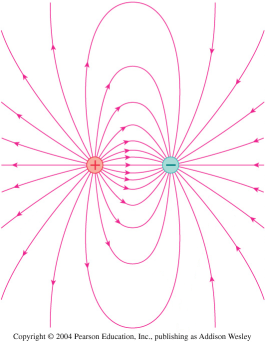You will find equipotential curves (cross-sections of equipotential surfaces) near a two-dimensional representation of an electric dipole. You will make a qualitative representation of electric field lines by sketching smooth curves from one charged particle
to the other, crossing each equipotential curve at a right angle.
Quantitatively, you will determine the electric field at points along a straight line between the two charged particles
. Since the field due to each particle is in the same direction along this line, the total field magnitude at each point is the sum of the individual field magnitudes.
Etotal = E- + E+ = kQ- / r-2 + kQ+ / r+2
In a dipole, the charge magnitudes are the same, so Q+ = Q- = Q. If the point at which the electric field is to be calculated is a distance x from the negatively charged particle, and the distance between the charged particles is d, then r- = x and r+ = d - x, so
Etotal =kQ / x2 + kQ / (d - x)2 = kQ [1 / x2 + 1 / (d - x)2]
That is, a graph of Etotal as a function of 1 / x2 + 1 / (d - x)2 is expected to be linear with slope kQ.