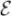Physics 2212, Lab 11: Induction

Eric Murray, Fall 2006

Required Advance Reading

Faraday's Law relates an induced emf, 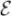, to an change in magnetic flux, dΦ / dt.

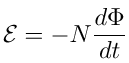
You'll be using two coils, a primary coil through which a sinusoidally varying current will flow, and a secondary coil in which an emf will be induced. This induced emf in the secondary depends on the number of turns in the secondary coil, N_s. Since the coils are coaxial, the varying magnetic flux Φ_p = ∫B_p⋅dA_p created by the current in the primary coil is the same as the varying flux Φ_s in the secondary coil.

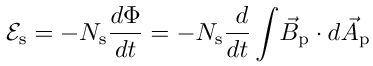
If the primary coil can be treated as an infinite solenoid, then the magnetic field is parallel to, and uniform over, a cross-sectional area element

and the magnetic field magnitude is B_p = μ₀In_p, where n_p is the linear turn density N_p/l_p of the primary

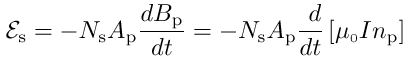
μ₀ and n_p do not depend on time, but the current varies sinusoidally, so

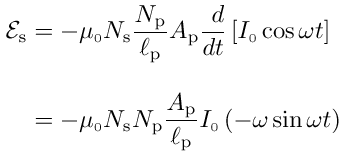
The peak value of the induced emf, 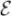_s0, occurs when sin(ωt) = 1

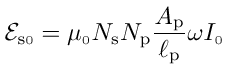
You will investigate the relationships between the amplitude of the induced emf, 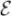_s0 and the amplitude of the applied current I₀, the frequency f of the applied current (remember that ω = 2πf ), and length l_p of the primary coil inside the secondary.