Eric Murray, Fall 2006
An object moving along a circular path has an acceleration toward the center with magnitude ac given by
ac = vt2 / r = ω² r
where vt is the tangential component of the velocity, ω is the magnitude of the angular velocity (in radians per unit time), and r is the distance of the object from the circle's center.
The acceleration toward the center, or centripetal acceleration, is only the same as the total
acceleration if the tangential acceleration is zero. An object with constant angular velocity,
and thus constant tangential velocity magnitude, would have zero tangential acceleration. You
should be able to think of other situations in which an object's tangential acceleration is zero,
if only momentarily.
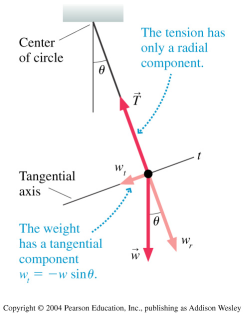
You will record the force (T in the diagram) on a rod supporting a block, as it swings through a circular arc like a pendulum. The oscillations of this pendulum will be damped, so the amplitude changes with time. The mass, however, is constant, so mass is the parameter you will calculate using Newton's Second Law,
∑Fc = m ac
from the measured force and angular velocity at particular instants. Think about how those instants should be chosen to make this calculation easy to perform.