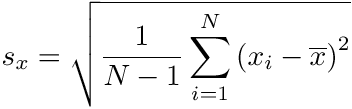
Eric Murray, Fall 1999
If you were to ask someone their height, and they responded with "six feet," how well do you think you’d know their height? They probably haven’t been measured to the nearest mil (one-thousandth of an inch) to be 6 ft 0.000 in. Maybe you’d expect them to be somewhere between 5 ft 11.5 in and 6 ft 0.5 in. Or between 5 ft 11 in and 6ft 1in. Or maybe even just somewhere between 5 ft 6 in and 6 ft 6 in.
The problem here is that no range indicating the quality of the measurement, or experimental uncertainty, has been assigned to the quantity, 6 ft.
Really, 6 ft
is only slightly more helpful than the utterly meaningless response 6
would be. A much better response would be 72 ± 2 in
where the experimental uncertainty is 2 in, and now you know that their height is probably between 5 ft 10 in and 6 ft 2 in.
In the physical sciences, this becomes very important when trying to decide whether or not an experimental result agrees with theory. For example, theory tells you that an object dropped near the Earth’s surface will have a speed of 4.9 m/s one second after it is released (on a flat, airless, motionless Earth). Does a measurement of 5.2 m/s agree with theory? What about a measurement of 4.0 m/s? The fact is, you can’t tell without an estimate of the experimental uncertainty. If the 5.2 m/s is 5.2 ± 0.1 m/s, it does not agree. If the 4.0 m/s is 4.0 ± 1.0 m/s, it may be a sloppily performed experiment, but it does agree.
Experimental uncertainties are estimates of the amount of random error present in a particular experiment. Random errors are present in any experiment, and are the things you have no control over. They are the things that can go either way,
that is, either increasing or decreasing a result. An example would be timing something with a stopwatch—you may hit the stop button a little too soon, or a little too late. If you measure something only once, it is up to you to estimate the experimental uncertainty based on your judgement of the quality of the measurement. It is your measurement, and no one knows better than you how well it was taken.
Much less subjective, however, is to estimate the experimental uncertainty by statistical analysis of multiple measurements of the same quantity. The more times you measure a particular quantity, the more you should know about the true
value of that quantity. (The true
value, of course, is inherently unknowable. Although we trust that there is a true
value, all we can know are the values of our measurements.) Suppose two groups of students each repeat a certain process six times, measure its duration, and record the following results:
|
|
|||||||||||||||||||||||||||||||||||||||||
Group B’s data appears to have no variation, that is, their experiment has no random error. They need to either get a digital stopwatch with more precision, or try to estimate between the marks of an analog stopwatch. Their data is not useful, and they should repeat their experiment.
Group A’s data, however, is different. It seems to fluctuate around some value. Given these measurements, what would be your best estimate of the true
duration of the process they are timing? Hopefully, it would make sense to claim the arithmetic mean (7.99 s). As a first step toward finding out how close to the true
value we expect the arithmetic mean to be, we can measure the scatter in the data by calculating the standard deviation according to:
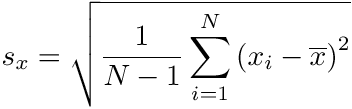
where sx is the standard deviation of the measurements of some quantity x (strictly speaking, the sample standard deviation, as opposed to the population standard deviation), N is the number of measurements taken, xi takes on the value of each individual measurement, and
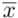is the arithmetic mean of the measurements. (You should note that calculating the standard deviation assumes that the measurements are independent, that is, that the random error in one trial does not affect any of the others.) Once enough measurements are taken, the standard deviation should remain roughly constant (that is, not change as more measurements are made), as it is a measure of the random errors present in the experiment. The standard deviation of Group A’s measurements is 0.02 s, which tells us (we state without proof or explanation, but you can check it out in an elementary statistics text or course) that we expect about 68% of the data (five or six of the eight measurements) to lie in the range 7.97 s to 8.01 s (within one standard deviations from the mean). You will note that five of Group A’s data points do, in fact, lie within this range. Additionally, we expect about 95% of the data (seven or eight of the measurements) to lie in the range 7.95 s to 8.03 s (within two standard deviations from the mean), and you will note that all eight of the measurements do, in fact, lie within this range.
This is all well and good, but ultimately, we do not want to know about the scatter in the data, but about how close we expect the true
value to be to the mean we have calculated. Also, a measure that approaches some constant as we take more measurements doesn’t help, as we’d certainly expect to have a better and better grasp on the true
value as more and more measurements are taken. The standard error (sometimes called the standard deviation of the mean) is what we want, and it can be calculated according to:
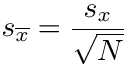
where
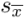is the standard error, sx is the standard deviation, and N is the number of measurements. You will note that, as the standard deviation tends toward some constant characteristic of the experiment as more measurements are taken, the standard error does get smaller. More measurements tell us more about the true
value of what we are trying to measure.
(An aside about significant figures is necessary here. While you do not want to report more figures than are significant, you should keep extra figures in your calculations to reduce accumulated round-off error. With some extra digits that won’t be reported, but will be used in calculations, then, the mean of Group A’s data, is 7.9863 s, while its standard deviation is 0.0239 s. Standard deviations and standard errors should be reported with only one significant digit.)
The standard error in Group A’s data is 0.008 s. This is the estimate of the experimental uncertainty, due to random errors, in the measure of the true
value. You will note that the uncertainty appears in the thousandth’s place, even though each individual measurement was only made to the hundredth’s place. This is OK, as we expect the mean to contain more information about the true
value than any single measurement would have. Group A should keep enough significant digits in their mean so that the standard error matters. With a standard error of 0.008 s, more is known than 7.99 s shows. They should report their result as 7.986 ± 0.008 s. This means (again, without proof or explanation) that the probability is about 68% that the true
value lies in the range 7.978 s to 7.994 s (within one standard error from the mean) and the probability is about 95% that the true
value lies in the range 7.970 s to 8.002 s (within two standard errors from the mean).
Consider the range two standard errors from the mean. If the theoretical value lies outside this range, and the probability is only 5% that the true
value lies outside the range (since the probability is 95% that it lies inside the range), one can claim that the theory does not agree with the experiment (or vice versa), and only be wrong 5% of the time. If one only looked at the range one standard error from the mean, one would be mistaken in such a claim 32% of the time. One can come up with other rates for making this mistake, such as 10% of the time using a range 1.65 standard errors from the mean, and one can certainly use more sophisticated statistical tests, but two standard errors, claiming disagreement wrongly only 5% of the time
is a quick, easy, and reasonable test. One should report, then, the mean plus or minus one standard error as one’s result, but should check a range of two standard errors each way when deciding whether or not theory and experiment agree.
In addition to random errors, which can make results either too high or too low and can be measured statistically, there are also systematic errors, which tend to operate in only one direction, and cannot be treated with statistics. Systematic errors are a sign that something is wrong, either the theory (such as using a theory that neglects friction in an environment in which there is friction), or the equipment (such as measuring lengths with a meter stick that has a couple of millimeters worn off the end). You will note that these effects always act the same way, friction always making objects move slower and not as far as they would without it, and the meter stick consistently overstating lengths by a couple of millimeters. Because these effects are consistent, they cannot be measured with statistics, and can only be dealt with by thinking carefully about your experiment and your theory.
(Another situation that often looks like a systematic error is a simple math mistake. If you are calculating the volume of spheres from their diameters, and you leave the π out of the equation, your results will always be too small by a factor of π. This looks like a systematic error, which is a hint that something is wrong, and your careful thought should then lead you to correcting the mistake.)
If theory and experiment differ by more than the estimate of random error (two standard errors), the excess must be due to systematic error. Ultimately, if all the equipment is working properly, and theory includes every effect that we know of, and there is still a systematic error, then there must be some effect that we do not know of, and the theory must be adjusted to include it. This is how scientific knowledge is advanced.