Eric Murray, Fall 1999
Questions these experiments will enable you to answer: How long does it take my cart to roll down the track? Does this agree with theory? How many trials must be performed for a statistical analysis of random error to be valid?
Features: The object is a cart on a track (a one-dimensional space) with negligible friction. The measurement only involves the experimenter, a ruler, and a stop-watch.
Approach: The track is converted to a ramp by raising one end by some suitable method and starting the cart from close to the high end of the track. Measurements are made using a ruler (on the track) and a stopwatch, for a particular coasting distances down the track. You should think about the best way to divide tasks among lab partners to minimize the effect that your reaction time operating the stopwatch has on your measurements.
Method: Level your track, then raise one end by placing one set of supports on the upper level of your riser block. Record the separation of the supports, and the height of your riser block. Start the cart from rest at a chosen position (front end of cart relative to ruler, say) and measure the time to travel a fixed (and recorded) distance (at least 1.5 m) down the track After each trial (beginning with the second), calculate the average and the standard deviation of the travel times so far. For the second and third trials, you should calculate the standard deviation according to the equation in the prelab. For the third and subsequent trials, you may use a function in your calculator or in a computer spreadsheet. (Calculating the standard deviation after the third trial both ways is a check, perhaps of your calculating ability, but also that you are using your calculator or computer properly.) Repeat your measurement of travel times until the standard deviation seems to have reached a constant. If it reaches a constant after only a few trials, you should perform at least ten, anyway.
Comparison to theory: Assuming that the only unbalanced force on the cart is a component of gravity pulling it down the track, theory (that you will study later in the course) states that the time, t, for your cart to roll a distance, d, along the track is
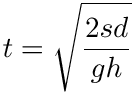
where h is the height of the riser block, s is the separation of the track supports, and g is the acceleration of gravity near the Earth’s surface (9.81 m/s2). Does your experiment agree with theory, that is, does the theoretical prediction lie within two standard errors from the experimental mean? If it does not, you should think about what systematic errors might have caused the difference. In any case, you should think about what random errors might have contributed to the standard error.
Summary: Review your worksheet. Think about the goals of these experiments, your results, and the expectations from theory while writing your discussion.